Spectral (FFT) analysis
xr-scipy wraps some of scipy spectral analysis functions such as scipy.signal.spectrogram(), scipy.signal.csd() etc. For convenience, the xrscipy.signal namespace will be imported under the alias dsp
In [1]: import xrscipy.signal as dsp
In [2]: import xrscipy.signal.extra as dsp_extra
To demonstrate the basic functionality, let’s create two simple example DataArray at a similar frequency but one with a frequency drift and some noise:
In [3]: time_ax = np.arange(0,100,0.01)
In [4]: sig_1 = xr.DataArray(np.sin(100 * time_ax) + np.random.rand(len(time_ax))*3,
...: coords=[("time", time_ax)], name='sig_1')
...:
In [5]: sig_2 = xr.DataArray((np.cos(100 * time_ax) + np.random.rand(len(time_ax))*3 +
...: 3*np.sin(30 * time_ax**1.3)),
...: coords=[("time", time_ax)], name='sig_2')
...:
Power spectra
The spectrogram() function can be used directly on an xarray
DataArray object. The returned object is again an xarray.DataArray object.
In [6]: spec_1 = dsp.spectrogram(sig_1)
In [7]: spec_2 = dsp.spectrogram(sig_2)
In [8]: spec_2
Out[8]:
<xarray.DataArray 'spectrogram_sig_2' (frequency: 129, time: 77)>
array([[2.44424801e-05, 5.22947169e-03, 2.89224670e-04, ...,
1.49873467e-03, 7.65608700e-04, 9.59582636e-05],
[1.75153585e-02, 1.89154990e-02, 7.80560915e-03, ...,
1.44778153e-03, 1.09230319e-02, 9.86477734e-03],
[2.67981444e-02, 1.72320528e-03, 1.77923215e-02, ...,
3.47197400e-03, 7.94489056e-05, 1.24722011e-02],
...,
[7.31455285e-03, 1.98518741e-02, 5.07390687e-03, ...,
6.44165409e-03, 5.43732551e-03, 7.00189408e-03],
[3.07786421e-03, 1.69232295e-03, 1.04356585e-03, ...,
2.04653030e-02, 5.20056837e-04, 1.61887611e-02],
[2.69532456e-03, 1.81679619e-05, 2.76618829e-03, ...,
5.93410480e-03, 6.43149358e-03, 1.45961774e-02]])
Coordinates:
* time (time) float64 1.28 2.56 3.84 5.12 6.4 ... 94.72 96.0 97.28 98.56
* frequency (frequency) float64 0.0 0.3906 0.7812 1.172 ... 49.22 49.61 50.0
The frequency dimension coords are based on the transformed dimension (time in this case) coords sampling (i.e. inverse units). When the signal is 1D, the dimension does not have to be provided.
In [9]: norm = plt.matplotlib.colors.LogNorm()
In [10]: plt.subplot(211)
Out[10]: <Axes: >
In [11]: spec_1.plot(norm=norm)
Out[11]: <matplotlib.collections.QuadMesh at 0x7f948f56ad90>
In [12]: plt.subplot(212)
Out[12]: <Axes: >
In [13]: spec_2.plot(norm=norm)
Out[13]: <matplotlib.collections.QuadMesh at 0x7f948f5d1650>
In [14]: plt.show()

These routines calculate the FFT on segments of the signal of a length controlled by nperseg and nfft parameters. The routines here offer a convenience parameter seglen which makes it possible to specify the segment length in the units of the transformed dimension’s coords. If seglen is specified, nperseg is then calculated from it and nfft is set using scipy.fftpack.next_fast_len (or to closest higher power of 2). A desired frequency resolution spacing df can be achieved by specifying seglen=1/df.
Another convenience parameter is overlap_ratio which calculates the noverlap parameter (by how many points the segments overlap) as noverlap = np.rint(overlap_ratio * nperseg)
For example, these parameters calculate the spectrogram with a higher frequency resolution and try to make for the longer segments by overlapping them by 75%.
In [15]: dsp.spectrogram(sig_1, seglen=1, overlap_ratio=0.75)
Out[15]:
<xarray.DataArray 'spectrogram_sig_1' (frequency: 51, time: 397)>
array([[3.99319244e-04, 5.72385049e-06, 4.63213189e-04, ...,
1.30700319e-03, 8.42935876e-04, 2.13630973e-03],
[2.36519351e-03, 2.63675999e-03, 2.70759396e-03, ...,
1.35248503e-02, 1.52467384e-02, 1.52477065e-02],
[1.14508286e-03, 6.57120911e-03, 1.59951326e-02, ...,
2.59556948e-02, 2.86589719e-02, 2.80344654e-02],
...,
[3.22485304e-02, 5.98876777e-03, 4.75008719e-03, ...,
1.27105913e-02, 1.10435949e-02, 2.60625766e-03],
[6.48727646e-03, 4.24654407e-03, 5.71875070e-03, ...,
3.54197551e-03, 4.97810155e-02, 5.84757962e-02],
[7.82088430e-04, 3.02992866e-04, 8.29188527e-03, ...,
1.46543043e-02, 4.78417261e-02, 3.80860346e-02]])
Coordinates:
* time (time) float64 0.5 0.75 1.0 1.25 1.5 ... 98.75 99.0 99.25 99.5
* frequency (frequency) float64 0.0 1.0 2.0 3.0 4.0 ... 47.0 48.0 49.0 50.0
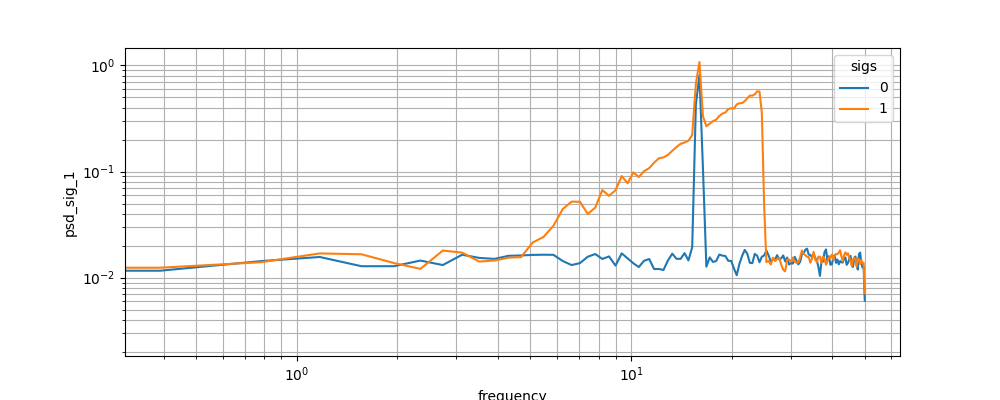
All the functions can be calculated on N-dimensional signals if the dimension is provided. Here the power spectral density (PSD) \(P_{xx}\) is calculated using Welch’s method (i.e. time average of the spectrogram) is shown
In [16]: sig_2D = xr.concat([sig_1,sig_2], dim="sigs")
In [17]: psd_2D = dsp_extra.psd(sig_2D, dim="time")
In [18]: psd_2D.plot.line(x='frequency')
Out[18]:
[<matplotlib.lines.Line2D at 0x7f948f5b0e10>,
<matplotlib.lines.Line2D at 0x7f948f5f3a90>]
In [19]: plt.loglog()
Out[19]: []
In [20]: plt.grid(which='both')
In [21]: plt.show()
Cross-coherence and correlation
The same windowed FFT approach is also used to calculate the cross-spectral density \(P_{xy}\) (using xrscipy.signal.csd()) and from it coherency \(\gamma\) as
where \(\langle \dots \rangle\) is an average over the FFT windows, i.e. ergodicity is assumed.
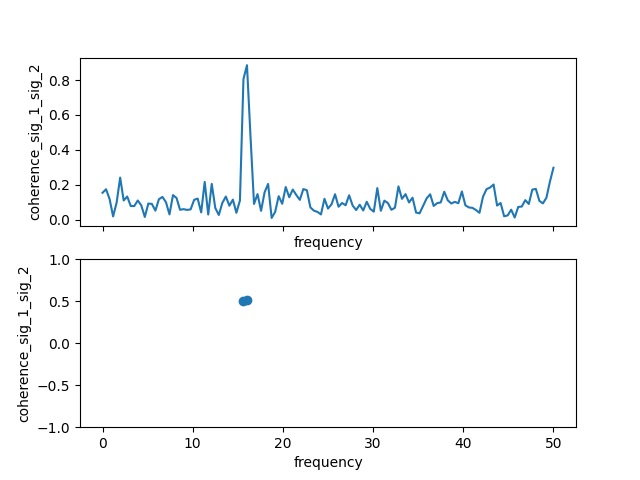
In [22]: coher_12 = dsp.coherence(sig_1, sig_2)
In [23]: coher_12[:10]
Out[23]:
<xarray.DataArray 'coherence_sig_1_sig_2' (frequency: 10)>
array([ 0.15445836+0.j , 0.09626349+0.14572021j,
0.01668929+0.1171455j , -0.01160877+0.0149668j ,
-0.01835304-0.09690598j, 0.05856481-0.23405385j,
-0.10611867-0.03007782j, -0.08271153-0.10426975j,
0.01914803-0.07631421j, 0.0691541 -0.03660832j])
Coordinates:
* frequency (frequency) float64 0.0 0.3906 0.7812 1.172 ... 2.734 3.125 3.516
The returned \(\gamma\) DataArray is complex (because so is \(P_{xy}\)) and the modulus is what is more commonly called coherence and the angle is the phase shift.
In [24]: coh = np.abs(coher_12)
In [25]: xphase = xr.apply_ufunc(np.angle, coher_12) / np.pi
In [26]: fig, axs = plt.subplots(2, 1, sharex=True)
In [27]: coh.plot(ax=axs[0])
Out[27]: [<matplotlib.lines.Line2D at 0x7f948f201390>]
In [28]: xphase.where(coh > 0.6).plot.line('o--', ax=axs[1])
Out[28]: [<matplotlib.lines.Line2D at 0x7f948f3de190>]
In [29]: axs[1].set(yticks=[-1, -0.5, 0, 0.5, 1]);
In [30]: plt.show()
In the future more convenient wrappers returning the coherence magnitude and cross-phase might be developed.
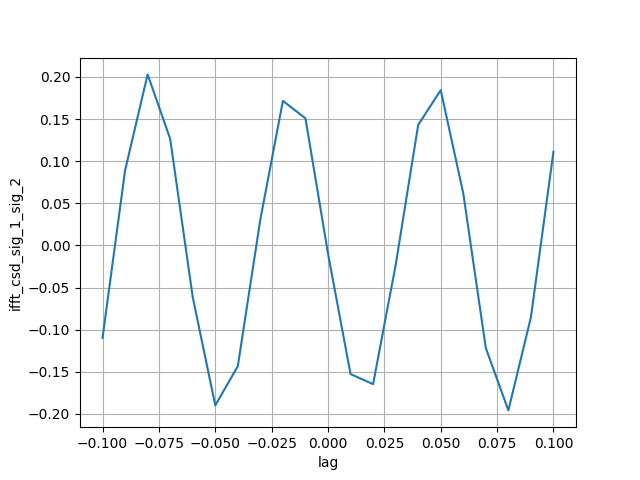
The cross-correlation is calculated similarly as \(\gamma\), but with \(\mathcal{F}^{-1} [\langle P_*\rangle ]\), i.e. in the inverse-FFT domain. The lag coordinates are the inverse of the frequency coordinates.
In [31]: xcorr_12 = dsp_extra.xcorrelation(sig_1, sig_2)
In [32]: xcorr_12.loc[-0.1:0.1].plot()
Out[32]: [<matplotlib.lines.Line2D at 0x7f948f21d1d0>]
In [33]: plt.grid()
In [34]: plt.show()
A partially averaged counterpart to coherence() is coherogram() which uses a running average over nrolling FFT windows.