Digital filters
xr-scipy wraps some of SciPy functions for constructing frequency filters using functions such as scipy.signal.firwin() and scipy.signal.iirfilter(). Wrappers for convenient functions such as scipy.signal.decimate() and scipy.signal.savgol_filter() are also provided.
For convenience, the xrscipy.signal namespace will be imported under the alias dsp:
In [1]: import xrscipy.signal as dsp
In [2]: import xrscipy.signal.extra as dsp_extra
Frequency filters
The main wrapper for frequency filters is the frequency_filter() wrapper. Its many arguments enable one to specify the type of filter, e.g. frequency band, FIR or IIR, response type family, filter order, forward-backward filtering, etc. By default a Butterworth IIR 4-th order filter with second-order-series (numerically stable even for high orders) forward-backward application (zero phase shift, but double order) is used, because such a filter typically offers a good performance for most time-series analysis applications.
Convenience functions such as lowpass(), highpass() and bandpass() are provided which wrap frequency_filter() with a predefined response type and offer a more convenient interface for the cutoff frequency specification.
The cutoff frequency is specified in the inverse usint to the filtered dimension’s coordinates (typically time). The wrapper automatically checks the sampling of those coordinates and normalizes the supplied frequency by the Nyquist frequency.
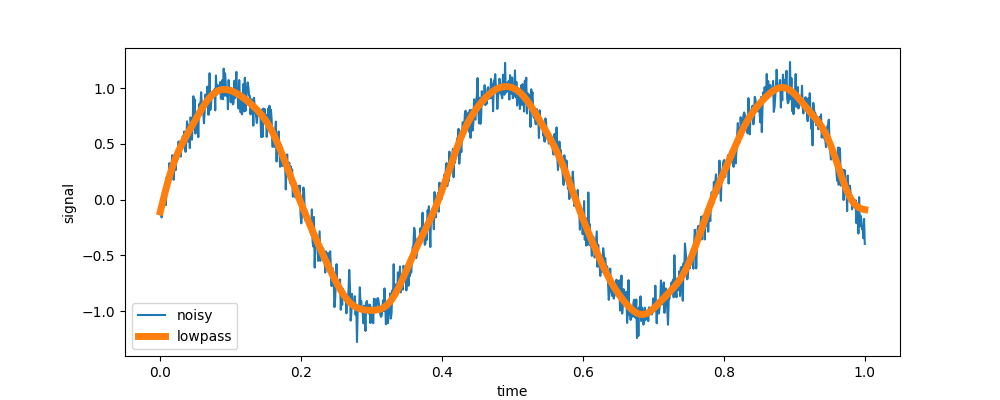
In the following example a simple low-pass filter is applied to a noisy signal. Because the cutoff frequency is close to 0 (relative to the Nyquist frequency) a high filter order is used for sufficient noise attenuation.
In [3]: t = np.linspace(0, 1, 1000) # seconds
In [4]: sig = xr.DataArray(np.sin(16*t) + np.random.normal(0, 0.1, t.size),
...: coords=[('time', t)], name='signal')
...:
In [5]: sig.plot(label='noisy')
Out[5]: [<matplotlib.lines.Line2D at 0x7fe8aff2c650>]
In [6]: low = dsp_extra.lowpass(sig, 20, order=8) # cutoff at 20 Hz
In [7]: low.plot(label='lowpass', linewidth=5)
Out[7]: [<matplotlib.lines.Line2D at 0x7fe8b40e8350>]
In [8]: plt.legend()
Out[8]: <matplotlib.legend.Legend at 0x7fe8b6799250>
In [9]: plt.show()
Decimation
To demonstrate basic functionality of decimate(), let’s create a simple example DataArray:
In [10]: arr = xr.DataArray(np.sin(np.linspace(0, 6.28, 300)) ** 2,
....: dims=('x'), coords={'x': np.linspace(0, 5, 300)})
....:
In [11]: arr
Out[11]:
<xarray.DataArray (x: 300)>
array([0.00000000e+00, 4.41075615e-04, 1.76352427e-03, 3.96501276e-03,
7.04165700e-03, 1.09880289e-02, 1.57971657e-02, 2.14605829e-02,
2.79682883e-02, 3.53088004e-02, 4.34691683e-02, 5.24349947e-02,
6.21904612e-02, 7.27183561e-02, 8.40001050e-02, 9.60158036e-02,
1.08744253e-01, 1.22162995e-01, 1.36248356e-01, 1.50975485e-01,
1.66318399e-01, 1.82250028e-01, 1.98742264e-01, 2.15766010e-01,
2.33291231e-01, 2.51287007e-01, 2.69721587e-01, 2.88562448e-01,
3.07776350e-01, 3.27329391e-01, 3.47187076e-01, 3.67314370e-01,
3.87675760e-01, 4.08235325e-01, 4.28956790e-01, 4.49803597e-01,
4.70738966e-01, 4.91725960e-01, 5.12727552e-01, 5.33706689e-01,
5.54626357e-01, 5.75449647e-01, 5.96139821e-01, 6.16660376e-01,
6.36975107e-01, 6.57048172e-01, 6.76844156e-01, 6.96328134e-01,
7.15465730e-01, 7.34223179e-01, 7.52567388e-01, 7.70465991e-01,
7.87887410e-01, 8.04800909e-01, 8.21176647e-01, 8.36985732e-01,
8.52200273e-01, 8.66793426e-01, 8.80739444e-01, 8.94013722e-01,
9.06592841e-01, 9.18454608e-01, 9.29578094e-01, 9.39943674e-01,
9.49533061e-01, 9.58329335e-01, 9.66316978e-01, 9.73481896e-01,
9.79811449e-01, 9.85294470e-01, 9.89921285e-01, 9.93683730e-01,
9.96575168e-01, 9.98590497e-01, 9.99726161e-01, 9.99980157e-01,
9.99352038e-01, 9.97842910e-01, 9.95455437e-01, 9.92193830e-01,
...
9.91623187e-01, 9.95016898e-01, 9.97537249e-01, 9.99179794e-01,
9.99941634e-01, 9.99821427e-01, 9.98819383e-01, 9.96937271e-01,
9.94178411e-01, 9.90547671e-01, 9.86051457e-01, 9.80697701e-01,
9.74495849e-01, 9.67456842e-01, 9.59593101e-01, 9.50918498e-01,
9.41448338e-01, 9.31199330e-01, 9.20189556e-01, 9.08438441e-01,
8.95966716e-01, 8.82796387e-01, 8.68950689e-01, 8.54454050e-01,
8.39332047e-01, 8.23611360e-01, 8.07319725e-01, 7.90485884e-01,
7.73139539e-01, 7.55311293e-01, 7.37032600e-01, 7.18335711e-01,
6.99253611e-01, 6.79819967e-01, 6.60069067e-01, 6.40035756e-01,
6.19755380e-01, 5.99263719e-01, 5.78596927e-01, 5.57791467e-01,
5.36884044e-01, 5.15911547e-01, 4.94910977e-01, 4.73919386e-01,
4.52973809e-01, 4.32111201e-01, 4.11368368e-01, 3.90781909e-01,
3.70388143e-01, 3.50223052e-01, 3.30322213e-01, 3.10720737e-01,
2.91453207e-01, 2.72553616e-01, 2.54055309e-01, 2.35990924e-01,
2.18392330e-01, 2.01290577e-01, 1.84715838e-01, 1.68697356e-01,
1.53263391e-01, 1.38441175e-01, 1.24256858e-01, 1.10735466e-01,
9.79008540e-02, 8.57756665e-02, 7.43812960e-02, 6.37378457e-02,
5.38640937e-02, 4.47774605e-02, 3.64939774e-02, 2.90282592e-02,
2.23934776e-02, 1.66013384e-02, 1.16620606e-02, 7.58435858e-03,
4.37542673e-03, 2.04092654e-03, 5.84976768e-04, 1.01461475e-05])
Coordinates:
* x (x) float64 0.0 0.01672 0.03344 0.05017 ... 4.95 4.967 4.983 5.0
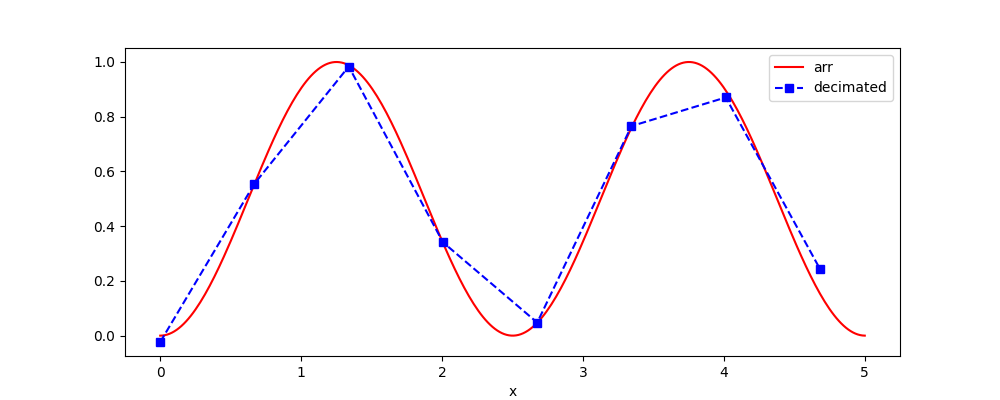
Our decimate() takes an xarray object
(possibly high dimensional) and a dimension name (if not 1D)
along which the signal should be decimated. Decimation means
Apply a lowpass filter to remove frequencies above the new Nyquist frequency in order to prevent aliasing
Take every q-th point
In [12]: arr_decimated = dsp.decimate(arr, q=40)
In [13]: arr_decimated
Out[13]:
<xarray.DataArray (x: 8)>
array([-0.02324268, 0.55546594, 0.98349812, 0.34108733, 0.04773383,
0.76581061, 0.87046882, 0.2435029 ])
Coordinates:
* x (x) float64 0.0 0.6689 1.338 2.007 2.676 3.344 4.013 4.682
An alternative parameter to q is target_fs which is the new target sampling frequency to obtain, q = np.rint(current_fs / target_fs).
The return type is also a DataArray with coordinates.
In [14]: arr.plot(label='arr', color='r')
Out[14]: [<matplotlib.lines.Line2D at 0x7fe8b40c9cd0>]
In [15]: arr_decimated.plot.line('s--', label='decimated', color='b')
Out[15]: [<matplotlib.lines.Line2D at 0x7fe8aff39250>]
In [16]: plt.legend()
Out[16]: <matplotlib.legend.Legend at 0x7fe8aff74910>
In [17]: plt.show()
The other keyword arguments are passed on to lowpass().
Savitzky-Golay LSQ filtering
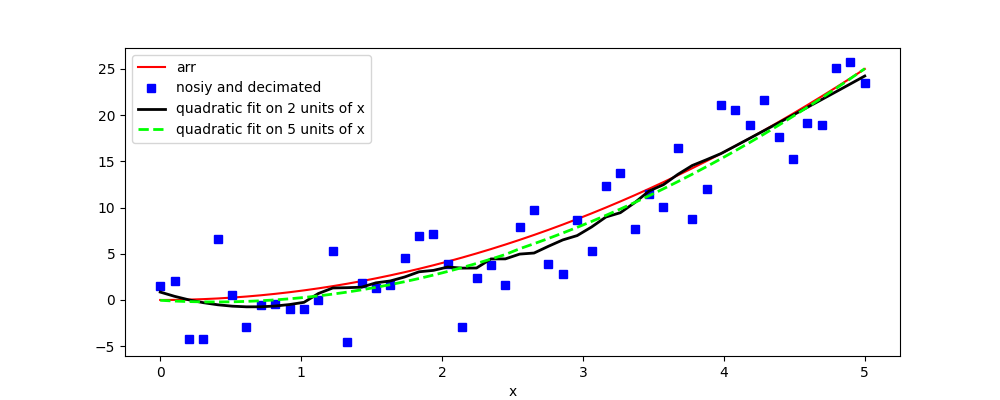
The Savitzky-Golay filter as a special type of a FIR filter which is equivalent to replacing filtered values by least-square fits of polynomials (or their derivatives) of a given order within a rolling window. For details see their Wikipedia page Such a filter is very useful when temporal or spatial features in the signal are of greater interest than frequency or wavenumber bands, respectively.
To demonstrate basic functionality of savgol_filter(), let’s create a simple example DataArray of the quadratic shape and add some noise:
In [18]: arr = xr.DataArray(np.linspace(0, 5, 50) ** 2,
....: dims=('x'), coords={'x': np.linspace(0, 5, 50)})
....:
In [19]: noise = np.random.normal(0,3,50)
In [20]: arr_noisy = arr + noise
In [21]: arr
Out[21]:
<xarray.DataArray (x: 50)>
array([0.00000000e+00, 1.04123282e-02, 4.16493128e-02, 9.37109538e-02,
1.66597251e-01, 2.60308205e-01, 3.74843815e-01, 5.10204082e-01,
6.66389005e-01, 8.43398584e-01, 1.04123282e+00, 1.25989171e+00,
1.49937526e+00, 1.75968347e+00, 2.04081633e+00, 2.34277384e+00,
2.66555602e+00, 3.00916285e+00, 3.37359434e+00, 3.75885048e+00,
4.16493128e+00, 4.59183673e+00, 5.03956685e+00, 5.50812162e+00,
5.99750104e+00, 6.50770512e+00, 7.03873386e+00, 7.59058726e+00,
8.16326531e+00, 8.75676801e+00, 9.37109538e+00, 1.00062474e+01,
1.06622241e+01, 1.13390254e+01, 1.20366514e+01, 1.27551020e+01,
1.34943773e+01, 1.42544773e+01, 1.50354019e+01, 1.58371512e+01,
1.66597251e+01, 1.75031237e+01, 1.83673469e+01, 1.92523948e+01,
2.01582674e+01, 2.10849646e+01, 2.20324865e+01, 2.30008330e+01,
2.39900042e+01, 2.50000000e+01])
Coordinates:
* x (x) float64 0.0 0.102 0.2041 0.3061 ... 4.694 4.796 4.898 5.0
Our savgol_filter() takes an xarray object
(possibly high dimensional) and a dimension name (if not 1D)
along which the signal should be filtered.
The window length is given in the units of the dimension coordinates.
In [22]: arr_savgol2 = dsp.savgol_filter(arr_noisy, 2, 2)
In [23]: arr_savgol5 = dsp.savgol_filter(arr_noisy, 5, 2)
In [24]: arr_savgol2
Out[24]:
<xarray.DataArray (x: 50)>
array([ 8.56203341e-01, 3.96395647e-01, 1.41459548e-02, -2.90545737e-01,
-5.17679429e-01, -6.67255121e-01, -7.39272812e-01, -7.33732502e-01,
-6.50634192e-01, -4.89977882e-01, -2.51763571e-01, 7.02067790e-01,
1.30020637e+00, 1.33302851e+00, 1.38572699e+00, 1.85653379e+00,
2.06074739e+00, 2.49014897e+00, 3.05217772e+00, 3.20485447e+00,
3.56841209e+00, 3.44974397e+00, 3.46125936e+00, 4.44487308e+00,
4.44708328e+00, 4.96773137e+00, 5.08244353e+00, 5.81362471e+00,
6.50226254e+00, 6.97100619e+00, 7.89901971e+00, 8.98203322e+00,
9.44445152e+00, 1.05323974e+01, 1.17935064e+01, 1.24788400e+01,
1.35918883e+01, 1.45515981e+01, 1.51849573e+01, 1.58435727e+01,
1.66685321e+01, 1.74966544e+01, 1.83279396e+01, 1.91623877e+01,
1.99999988e+01, 2.08407728e+01, 2.16847097e+01, 2.25318095e+01,
2.33820722e+01, 2.42354978e+01])
Coordinates:
* x (x) float64 0.0 0.102 0.2041 0.3061 ... 4.694 4.796 4.898 5.0
In [25]: arr_savgol5
Out[25]:
<xarray.DataArray (x: 50)>
array([-3.32337380e-02, -1.15598437e-01, -1.72851319e-01, -2.04992385e-01,
-2.12021634e-01, -1.93939066e-01, -1.50744681e-01, -8.24384804e-02,
1.09795374e-02, 1.29509372e-01, 2.73151023e-01, 4.41904491e-01,
6.35769775e-01, 8.54746876e-01, 1.09883579e+00, 1.36803653e+00,
1.66234908e+00, 1.98177345e+00, 2.32630963e+00, 2.69595763e+00,
3.09071745e+00, 3.51058909e+00, 3.95557254e+00, 4.42566781e+00,
4.92087489e+00, 5.54817753e+00, 6.09173275e+00, 6.65861004e+00,
7.24880940e+00, 7.86233084e+00, 8.49917436e+00, 9.15933995e+00,
9.84282761e+00, 1.05496373e+01, 1.12797692e+01, 1.20332230e+01,
1.28099990e+01, 1.36100970e+01, 1.44335171e+01, 1.52802593e+01,
1.61503236e+01, 1.70437099e+01, 1.79604183e+01, 1.89004488e+01,
1.98638013e+01, 2.08504759e+01, 2.18604726e+01, 2.28937914e+01,
2.39504322e+01, 2.50303952e+01])
Coordinates:
* x (x) float64 0.0 0.102 0.2041 0.3061 ... 4.694 4.796 4.898 5.0
The return type is also a DataArray with coordinates.
In [26]: arr.plot(label='arr', color='r')
Out[26]: [<matplotlib.lines.Line2D at 0x7fe8affe4410>]
In [27]: arr_noisy.plot.line('s', label='nosiy and decimated', color='b')
Out[27]: [<matplotlib.lines.Line2D at 0x7fe8aff45fd0>]
In [28]: arr_savgol2.plot(label='quadratic fit on 2 units of x', color='k', linewidth=2)
Out[28]: [<matplotlib.lines.Line2D at 0x7fe8affedfd0>]
In [29]: arr_savgol5.plot.line('--',label='quadratic fit on 5 units of x', linewidth=2, color='lime')
Out[29]: [<matplotlib.lines.Line2D at 0x7fe8afff6810>]
In [30]: plt.legend()
Out[30]: <matplotlib.legend.Legend at 0x7fe8afff6990>
In [31]: plt.show()
The other options (polynomial and derivative order) are the same as for scipy.signal.savgol_filter(), see savgol_filter() for details.